数据结构和算法

Zhang21 收录于 programming

2024-12-01 约 14032 字预计阅读 29 分钟

熟悉常见的数据结构和算法。

参考：

概述

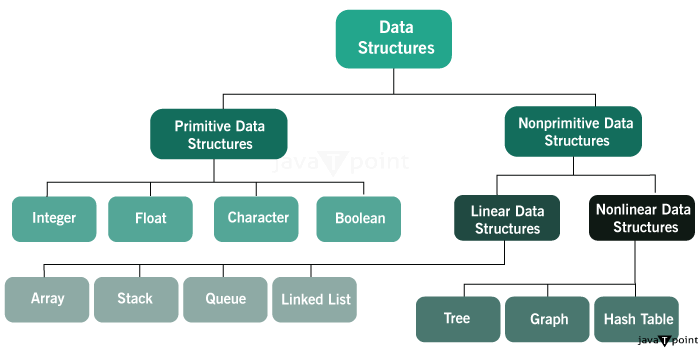
数据结构（Data Structure）是一种存储和组织数据的方式，以便有效地（空间和时间）使用数据。

为了在内存中构建数据结构，人们提出了 N 种算法，所有这些算法都被称为抽象数据类型（ADT, abstract data types）。这些抽象数据类型是一组规则。

数据结构的常见操作：

搜索（Search）
排序（Sort）
插入（Insert）
更新（Update）
删除（Delete）

数据结构的优点：

效率
可重用性
抽象

选择数据结构时需要考虑的因素：

需要存储什么类型的数据？
操作成本。
内存使用。

介绍

数据结构的一些例子包括：数组（Array）、链接列表（Linked List）、栈（Stack）、队列（Queue）、树（Tree）、图（Graph）等。

数据结构是计算机算法的主要部分，它们允许程序员有效地管理数据，在提高软件和程序性能有着重要的作用。

数据结构分类：

原始数据结构（Primitive）
非原始数据结构（Non-Primitive）

算法

算法（Algorithm）是一个问题的逻辑解决方案。

算法的特点：

输入（Input）
输出（Output）
明确性（Unambiguity）
有限性（Finiteness）
有效性（Effectiveness）
与语言无关

算法的数据流：

问题
算法
输入
处理单元
输出

算法因素：

模块化（Modularity）
正确性（Correctness）
可维护性（Maintainability）
功能性（Functionality）
鲁棒性（Robustness）
用户友好（User-friendly）
简单（Simplicity）
可扩展性（Extensibility）

算法方法：

蛮力算法
分而治之
贪婪算法
动态编程
分支与边界算法
随机算法
回溯

算法的主要类别：

排序
搜索
删除
插入
更新

算法复杂度：

时间复杂度（time complexity）：完成执行所需的时间，用大 O 表示。
空间复杂度（space completely）：解决问题并产生输出所需的空间大小。

渐进分析

理想的数据结构是在执行所有操作时占用尽可能少的时间或内存空间。我们的重点是找到时间复杂度，就能决定哪种数据结构最适合算法。

时间复杂度取决于输入的大小。因此，如果输入大小为 n，那么 f(n) 是表示时间复杂度的 n 的函数。

1
2
3
4
5
6


# 例如 f(n) = 5n^2 + 6n + 12
# 当 n 值越大时，其他两项就可以忽略。因此 f(n) = 5n^2 

# 这里得到的是近似时间复杂度（渐进复杂度），其结果与实际非常接近。
# 不计算精确的运行时间，而是提出不必要的项，只考虑耗时最长的项。

在数学分析中，算法渐近分析是一种定义算法运行时性能数学边界的方法。通过渐近分析，我们可以轻松得出算法的平均情况、最佳情况和最坏情况。

通常算法所需的时间分为三种情况：

最坏情况
平均情况
最佳情况

渐近符号

计算算法运行时间复杂度的常用渐近符号：

Big oh Notation (?)
Omega Notation (Ω)
Theta Notation (θ)

大 O 符号给出了函数的最小上界，使函数的增长速度永远不会超过这个上界。

大 O 符号的目的是给出特定函数的上限，并最终得出最坏的时间复杂度。

大 Ω 符号表示算法运行时间下限的正式方法，或者说是最佳情况下的时间复杂度。

大 Θ 符号表达算法运行时间上限和下限的正式方法，主要描述平均情况，介于最好和最坏情况之间。

因此，三种不同的分析为实际函数之间提供了适当的界限，确保算法不会超出这些界限。

指针

指针（Pointer）用于指向存储在计算机内存中任意位置的值的地址。

指针可提高重复性程序的性能：

遍历字符串
查找表
控制表
树状结构

指针细节：

指针运算：有四种运算符可用于指针：++, --, +, -
指针数组：可以定义数组来保存多个指针
指针到指针：C 语言允许在指针上设置指针。
C 中向函数传递指针
C 中从函数返回指针

结构体

结构体（Structure）是一种复合结构，它定义了一组变量列表，这些变量将以一个名称置于内存块中。结构体允许使用指向结构体的单一指针访问不同的变量。

可以容纳不同数据类型的变量
可以创建包含不同类型属性的对象
允许在不同程序中重用数据布局
用于实现其他数据结构，如链表、栈、丢列、树、图等。

1
2
3
4
5
6


struct structure_name
{
    data_type member1;
    data_type member2;
    ...
};

数组

数组（Array）被定义为存储在连续内存位置的同类数据项的集合。它是最简单的数据结构之一，每个数据元素都可以通过索引号随机访问。

数组属性

数组的一些属性：

数组中的每个元素都具有相同的数据类型和大小（4 bytes）。
数组中的元素存储在连续的内存位置，其中第一个元素存储在最小的内存位置。
由于可以根据给定的基础内存地址和数据元素的大小计算出数组中每个元素的内存地址，因此可以随机访问数组中的元素。
索引从 0 开始，可通过索引访问每个元素。

数组表示

在不同的编程语言中，可用不同的方式表示数组。

1
2


// c
int array [10] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

数组的优缺点

数组的优点：

对数组中的值进行排序和搜索更容易。
数组最适合快速轻松地处理多个值。
数组适合在单个变量中存储多个值，很容易记住单个名称。
遍历数组非常简单，只需要递增数据的基础地址，即可逐个访问每个元素。
使用索引可以直接访问数组中的任何元素。

数组的缺点：

数组是同质的，只有类型相同的元素才可以存储其中。
数组是静态内存分配，因此数组的大小不可更改。
如果存储的元素数量少于声明的大小，就会浪费内存。占用的内存大小在声明时就已经确定。

数组的内存分配

数组的所有元素存储在内存的连续位置，基地址是第一个元素的地址。

1
2
3
4
5


# int arr[5]
arr[0]    arr[1] arr[2] arr[3] arr[4]
100       104    108    112    116
base addr

访问数组元数

需要以下信息来访问数组中的任意随机元素：

数组的基础内存地址
元素的大小
索引类型

访问数组元素的地址的公式

1
2


Byte address of element A[i]  = base address + size * ( i - first index)

数组基本操作

数组支持的基本操作：

遍历：打印数组中的元素。
插入：在特定索引处添加元素。
删除：从特定索引中删除索引。
搜索：使用给定的索引或值搜索元素。
更新：更新特定索引中的元素。

数组操作的时间复杂度如下，空间复杂度是 O(n)。

操作	平均情况	最坏情况
访问	`O(1)`	`O(1)`
查找	`O(n)`	`O(n)`
插入	`O(n)`	`O(n)`
删除	`O(n)`	`O(n)`

二维数组

二维数据（2D Array）可定义为数组的数组，以矩阵的形式组织，可表示为行和列的集合。

二维数组是为了实现一种类似于关系数据库的数据结构。

1
2
3


// 声明一个 2d array
// int arr[行][列];
int arr[2][2] = {0, 1, 2, 3}

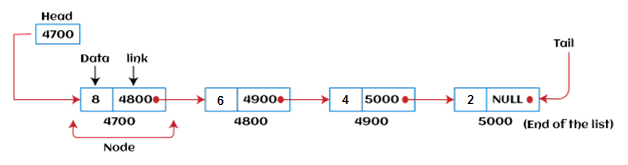
链表

链表（Linked list）是一种线性数据结构，包括一系列的相连的节点。链表可定义为随机存储在内存中的节点。链表中的节点包含两部分：第一部分是数据，第二部分是地址。列表中最后一个节点包含一个指向空的指针。

链表可表示为节点的连接，其中每个节点都指向了列表中的下一个节点。

为什么使用链表而不是数组？

使用数组之前，必须事先知道数组的大小。
增加数组的大小是一个耗时的过程。
数组的所有元素都需要连续存储在内存中。
在数组中插入一个元素需要移位其所有前置元素。
链表动态分配内存。链表中的所有节点都以非连续方式存储在内存中，并借助指针链接在一起。
在链表中，大小不再是问题。因为不需要在声明时定义其大小。列表会根据程序的需求增长，并受限于可用的内存空间。

链表的优缺点

链表优点：

动态数据结构：链表的大小可根据需要而变化，没有固定大小。
插入和删除很容易：只需要更新节点指针的地址即可，无需移位。
内存效率高：链表的大小可根据需要增大或缩小。
实现其他结构：可用链表来实现栈和队列。

链表缺点：

内存使用：链表的每个节点都占用两种变量，消耗更多的内存。
遍历：链表遍历并不容易。访问某个节点，需要遍历节点之前的所有节点，时间会很长。
反向遍历：链表反向遍历很困难。

声明链表

链表包含两个部分（一个简单变量，一个指针变量），两部分的类型都不同。

1
2
3
4


struct node {
    int data;
    struct node *next;
}

链表的应用

链表的应用场景：

多项式
稀疏矩阵
学生详情、员工详情或产品详情等
实现栈、队列、树和其他数据结构
实现动态内存分配

链表的操作

链表支持的基本操作：

插入
删除
显示
搜索

时间复杂度

操作	平均	最坏
插入	`O(1)`	`O(1)`
删除	`O(1)`	`O(1)`
搜索	`O(n)`	`O(n)`

空间复杂度

操作	空间复杂度
插入	`O(n)`
删除	`O(n)`
搜索	`O(n)`

链表的类型

链表分类：

单链表
双链表
循环链表
循环双链表

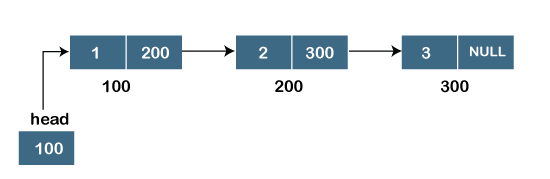
单链表

单链表（Singly Linked List），即常用的链表。包含两个部分：数据和地址（指针）。

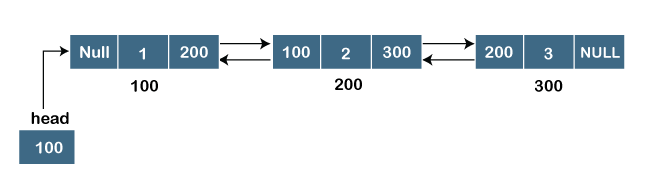
双链表

双链表（Doubly linked list），包含三个部分：数据和两个地址（一个指向上一个节点，一个指向下一个节点）。

循环链表

循环链表（Circular linked list），是单链表的一种变体。循环链表的最后一个节点连接到了第一个节点，因此它没有起点和终点节点。可以沿任何方向遍历（向前或向后）。

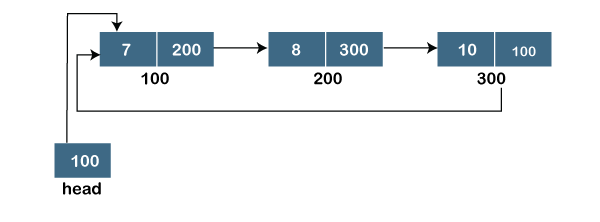
循环双链表

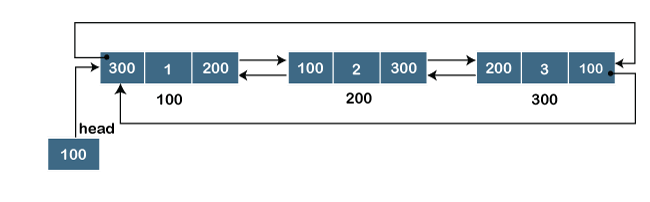
循环双链表（Doubly Circular linked list），是循环链表和双链表的结合。

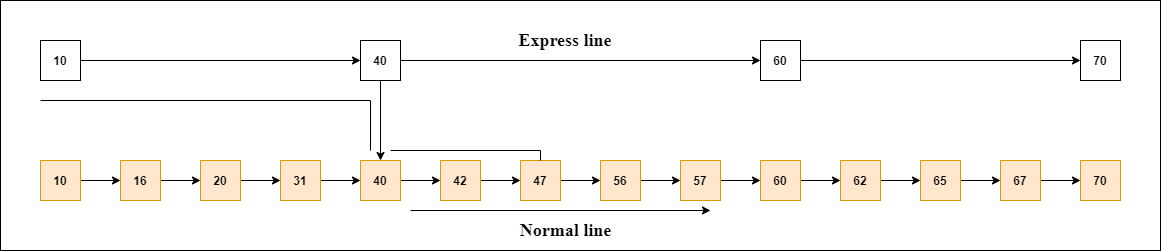
跳跃列表

跳跃列表（skip list）是一种概率数据结构。跳转列表是用链表来存储元素的排序列表。它允许高效地查看元素的处理过程。只需一步，它就能跳过整个列表中的多个元素，这就是它被称为跳过列表的原因。

跳转列表是链表的扩展版本。它允许用户快速搜索、删除和插入元素。它由一个基本列表组成，其中包括一组元素，该元素维护着后续元素的链接层次结构。

跳跃列表分为两层：最底层和顶层。最底层是一个普通的排序链表，而顶层就像一条快线，其中的元素会被跳过。

操作	平均	最坏
访问	`O(logn)`	`O(n)`
搜索	`O(logn)`	`O(n)`
删除	`O(logn)`	`O(n)`
插入	`O(logn)`	`O(n)`

栈

栈（Stack），是一种线性数据结构，遵循后进先出（LIFO）原则。栈只有一个端，包含一个指针，指向栈顶元素。每当在栈中添加一个元素时，它就会被添加到栈顶，而元素只能从栈中删除。插入和删除都只能从栈顶进行。

栈的一些要点：

称其为栈，是因为它的行为类似于现实世界中的对战、书堆等。
栈是一种抽象的数据类型，具有预定义的容量（存储大小有限的元素）。
按照特定顺序的数据结构，后进先出或先进后出。

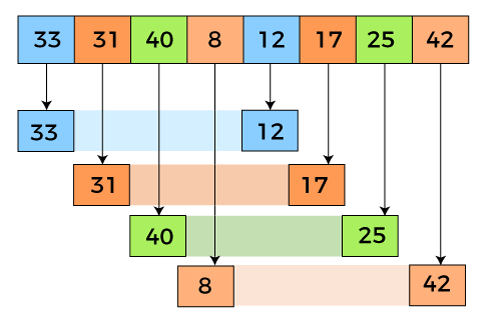
栈的工作模式

栈以后进先出的模式工作。如下图，栈的大小为 5。

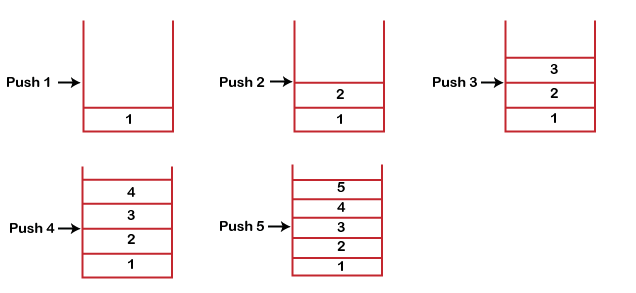
当在栈上执行删除操作时，由于另一端是关闭的，因此只有一种进入和退出方式。遵顼后进先出模式，后输入的值先删除后，才能删除之前的值。

栈的操作

栈上执行的一些常见操作：

push()：在栈中插入元素。如果栈已满，就会出现溢出。
pop()：从栈中删除元素。如果栈为空，此状态被称为下溢状态。
isEmpty()：判断栈是否为空。
isFull()：判断栈是否已满。
peek()：返回给定位置上的元素。
count()：返回栈中可用元素的总数。
change()：更改给定位置上的元素。
display()：打印栈中所有可用元素。

栈的应用

栈的一些应用场景：

符号平衡（Balancing of symbols）
字符串反转（String reversal）
UNDO/REDO
递归（Recursion）
深度优先搜索（Depth First Search）
回溯（Backtracking）
表达式转换（Expression conversion）
内存管理（Memory management）

栈的数组实现

通过数组实现栈，所有操作都是用数组执行。

栈的链表实现

通过链表实现栈。

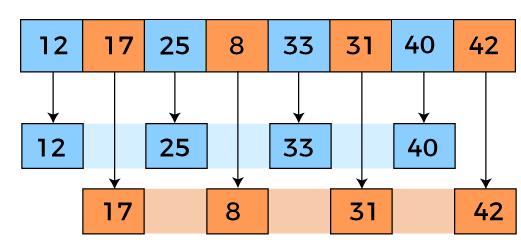
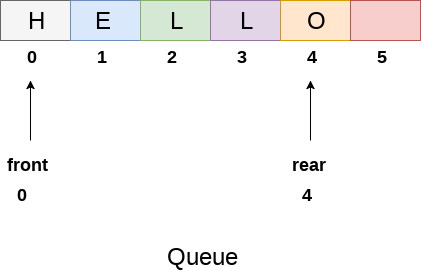
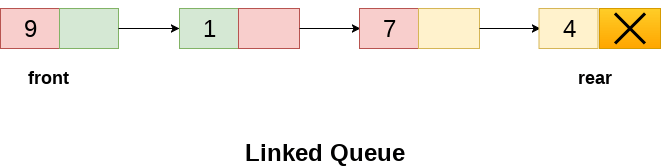
队列

队列可定义为一个有序列表，它在尾部插入元素，在首部删除元素。
队列称为先进先出（FIFO）列表。
例如，排队购买车票的人形成的一条队列。

队列的应用

队列被广泛用作单个共享资源（如打印机、磁盘）的等待列表。
队列用于异步传输数据（如管道、文件 IO 和 socket）。
队列在 MP3 播放器等应用程序中用作缓冲区。
队列用于维护在媒体播放器中的播放列表。
队列在操作系统中用于处理中断。

队列的复杂度

操作	平均	最坏
访问	`O(N)`	`O(N)`
搜索	`O(N)`	`O(N)`
插入	`O(1)`	`O(1)`
删除	`O(1)`	`O(1)`

队列类型

队列是一种数据结构，它遵循先进先出策略。队列也可定义为列表或集合。

在现实世界中，队列的例子是购票队列。先排队的人先拿到票，最后进入队列的人最后拿到票。

队列有 4种不同类型：

简单队列或线性队列
循环队列
优先队列
双端队列

线性队列

线性队列只能从后端插入，从前端删除。

由于先行队列只能从后端插入，如果队列中删除了前三个元素，即使队列中有可用空间，也无法插入更多元素。

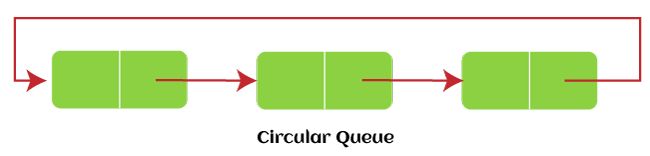
循环队列

循环队列中所有节点都表示为圆形。

循环队列可以克服线性队列的缺点。如果循环队列有空位，只需递增尾部值，就能在空位上添加新元素。使用循环队列的主要优点是能更好地利用内存。

优先级队列

其中的元素根据优先级排列，如果某些元素具有相同的优先级，则按照先进先出原则。

优先级队列，根据到达时间进行插入，根据优先级进行删除。优先队列主要用于 CPU 调度算法。

升序优先级队列
降序优先级队列

双端队列

Deque（或，双端队列），插入和删除可从队列的两端进行。

Deque 可用作回文检查器，如果我们从两端读取字符串，那么字符串将是相同的。

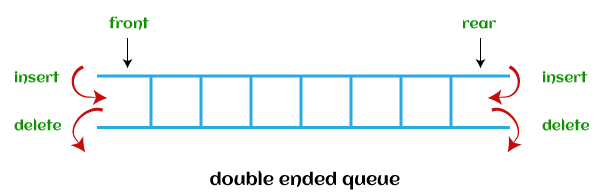
Input restricted deque：插入只能在一端进行，删除则可以两端进行。
Output restricted deque：删除只能在一端进行，插入则可以两端进行。

队列的操作

可对队列执行的基本操作：

Enqueue：将元素插入队列的后端。
Dequeue：从队列的前端删除元素。
Peek：返回队列中前置指针指向的元素，但不是删除元素。
Queue overflow (isfull)：队列满时的溢出情况。
Queue underflow (isempty)：队列为空时的下溢情况。

队列的数组实现

可以用线性数组轻松表示队列。

队列的链表实现

树

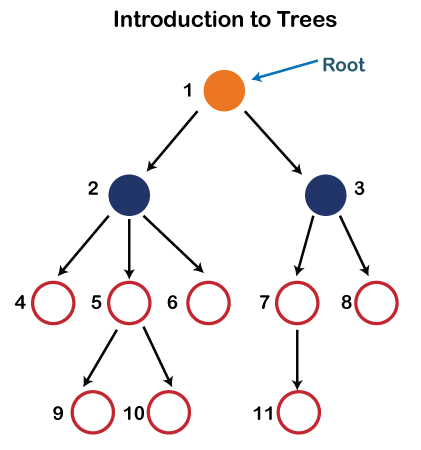
树（Tree），表示分层数据的数据结构。

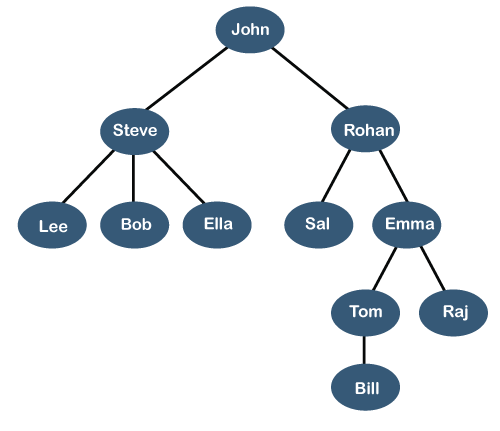
假设我们想以分层形式显示员工及其职位，可用以下表示：

树形结构的一些要点：

树形结构定义：是被称为节点（node）的对象的集合，它们连接在一起一表示层次结构。
树形结构是非线性的，它不是按顺序存储的。它是一种分层结构，因为树中的元素是按多层次排列的。
在树形结构中，最顶端的节点称为根节点。每个节点都包含一些数据（类型不限）。
每个节点都包含一些数据和其他节点（子节点）的链接。

树形结构中的一些基本术语：

Root：根节点是树层次结构中最顶端的节点。根节点没有父节点。
Child node：如果节点是任何节点的后代，他就是子节点。
Parent：如果节点包含子节点，他就是此节点的父节点。
Sibling：具有相同父节点的节点称为兄弟节点。
Leaf Node：没有子节点的节点称为叶子节点。叶子节点是树的最底层节点。
Internal node：一个节点至少有一个子节点，称为内部节点。
Ancestor node：祖先节点指从根节点到该节点上的任何前节点。
Descendant：给定节点的直接继承者，称为节点的后代。

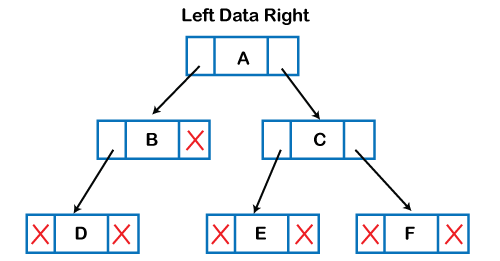
树的属性：

递归数据结构：树也被称为递归数据结构，因为树的根节点包含指向所有子树的链接。
边的数量：如果有 n 个节点，就有 $n-1$ 条边。
节点 x 的深度：节点 x 的深度可定义为从根节点到节点 x 的路径长度。根节点的深度为 0。
节点 x 的高度：节点 x 的高度可定义为从节点 x 到叶子节点的最长路径。

树形数据结构可以借助指针动态创建节点。

树形结构的应用场景：

存储自然分层数据：如文件系统中，文件和文件夹的形式自然是分层数据，并以树的形式存储。
组织数据：以便高效地插入、删除和搜索。如二叉树搜索一个元素的时间为 $logN$
Trie（字典树）：一种特殊的树，用于存储字典。
Heap（堆）：使用数组实现的树形结构。
B-Tree 和 B+Tree：两者都是树形数据结构，用于在数据库中实现索引。
路由表：用于在路由器中存储路由表。

树的类型：

普通树：一个节点可以有 0 个或最多 n 个节点。节点的度数（节点可包含的节点数）没有限制。子树是无序的，因为子树上的节点不能有序排列。
二叉树：树中的每个节点最多可以有两个子节点。最多指的是该节点有 0, 1, 2 个节点。
二叉搜索树：其中一个节点与 n 个节点相连。它是一种基于节点的数据结构。一个节点可用 3个字段来表示：数据部分、左子节点和右子节点。一个节点可连接到最多两个子节点，因此此节点包含两个指针。左侧子树中每个节点的值必须小于根节点，而右侧子树中每个节点的值必须大于根节点。
AVL 树：它是二叉搜索树的一种变体。它是一种自平衡二叉搜索树。自平衡指左子树和右子树的高度。
红黑树：它是一个自平衡的二叉搜索树。
倾斜树：它是一种自平衡的二叉搜索树。
Treap：源于树和堆数据结构，它同时包含了树和堆的属性。
B-tree：是一颗平衡的 m 向树，其中 m 定义了树的顺序。

二叉树

二叉树（Binary Tree），节点最多只能有两个子节点。这里的二进制表示两个的意思。因此，每个节点可以有0、1 或 2 个子节点。

二叉树的特性

每一级 i 的节点数最多为 $2^i$
高度 h 可能的最大节点数为 $2^{h+1}-1$
高度 h 可能的最小节点数为 $h+1$
如果节点数最小，那么树的高度就是最大。反之，如果节点数最大，那么树的高度就是最小。

二叉树的类型

二叉树：

严格/满（strict/full）二叉树
完全（complete）二叉树
完美（perfect）二叉树
退化（degenerate）二叉树
平衡（balanced）二叉树

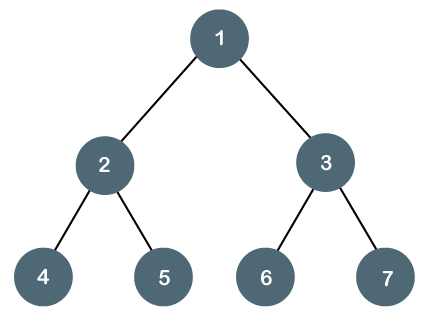
满二叉树

严格/满二叉树，除叶子节点外，每个节点必须包含 2 个子节点。

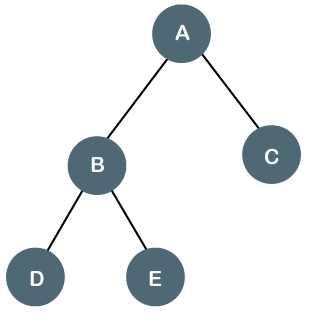
完全二叉树

完全二叉树，除了最后一级外，所有节点都被完全填满。所有节点必须尽可能靠左。在一棵完整二叉树中，节点应从左边开始添加。

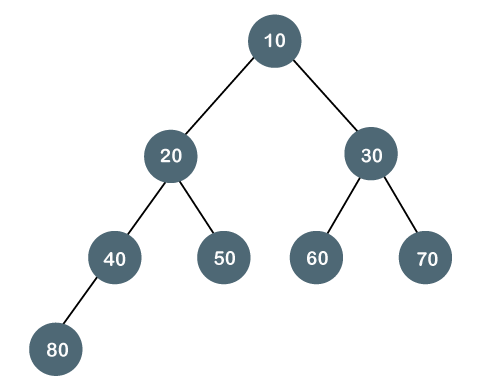
完美二叉树

完美二叉树，所有内部节点都有 2 个子节点，并且所有叶子节点都在同一层。

完美二叉树是完全二叉树，也是满二叉树。

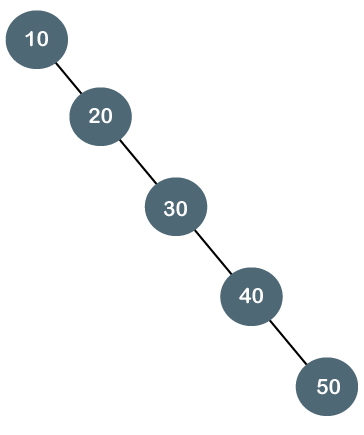
退化二叉树

退化二叉树，内部节点都只有一个子节点。

右斜树和左斜树。

平衡二叉树

平衡二叉树，每个节点的左右两子树的高度差都不超过 1 的树。例如 AVL 树和红黑树。

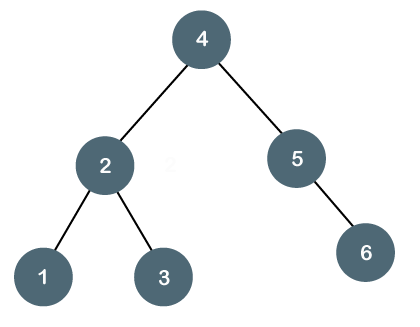
二叉搜索树

二叉搜索树（binary search tree），左节点的值必须小于父节点，右节点的值必须大于父节点。这条规则会递归应用到根节点的左右子树。

优点：

在二叉搜索树中非常容易，因为总能知道哪个子树中有所需要的元素。
与数组和链表相比，二叉搜索树的插入和删除操作速度更快。

二叉搜索树中的搜索：

首先，将要搜索的元素与根元素进行比较。
如果根节点匹配，则返回。
小于根元素，找左子树；大于跟元素，找右子树。
递归地重复上述步骤，知道找到匹配结果。
如果在树种未找到元素，则返回 NULL。

二叉搜索树中的删除，可能有三种情况：

要删除的节点是叶子
要删除的节点只有一个子节点：子节点成为此节点
要删除的节点有两个子节点：根据左右情况改变节点

二叉搜索树中插入新键，必须从根节点开始搜索，根据大小决定插入位置。

AVL树

AVL 由 Adelson Velsky 和 EM Landis 与 1962 年发明，该树被命名为 AVL，以纪念其发明者。

AVL 树可定义为高度平衡的二叉搜索树，其中每个节点都与平衡因子相关联，平衡因子是通过将其右侧子树的高度减去其左侧子树的高度计算出。

如果每个节点的平衡因子在 -1 到 1 之间，则树是平衡的。否则，该树不平衡，需要进行平衡。

B-Tree

B-Tree 是一种特殊的 m 向树，可广泛用于磁盘访问。阶数为 m 的 B 树中最多有 m-1 个键和 m 个子节点。使用 B-Tree 的一个主要原因是，它可以在单个节点中存储大量的键，并通过保持树的高度相对较小，存储大量的键值。

B-Tree 为数据编制索引，并提供对存储在磁盘上的实际数据的快速访问。因为访问存储在磁盘上的数据库的值是一个非常耗时的过程。

阶数 m 的 B-Tree 包含 m 向的特性：

每个节点最多包含 m 个子节点。
除了根节点和叶子节点外每个节点至少包含 m/2 个子节点。
根节点必须至少有 2 个节点。
所有叶子节点必须处于同一级别。

一个 4 阶的 B-Tree 示例图

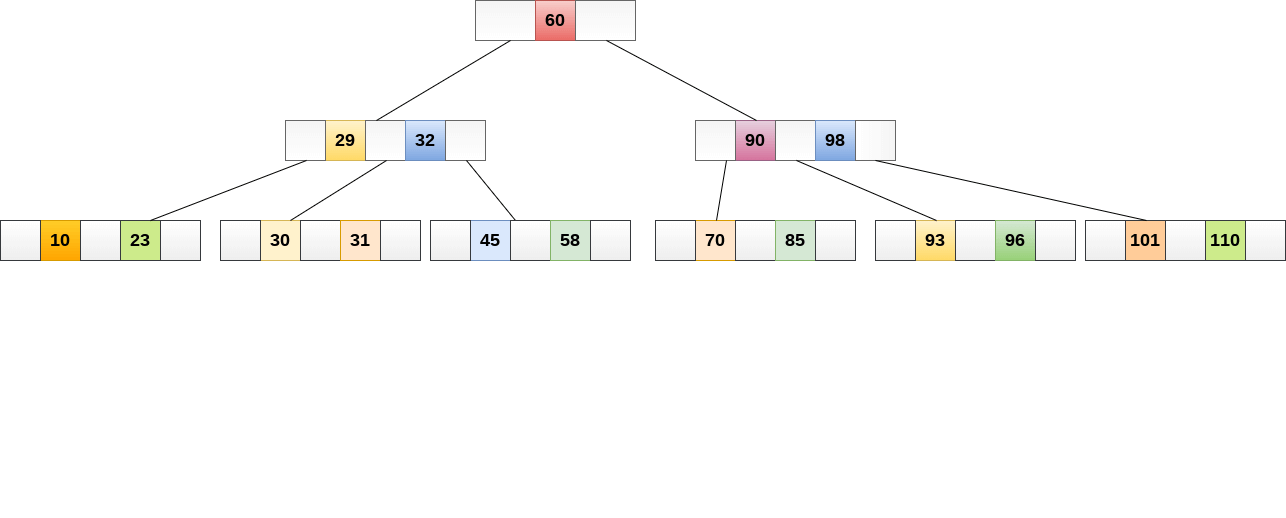
B+Tree

B+Tree 是 B-Tree 的扩展，可高效的插入、删除和搜索。

在 B-Tree 中，键和记录都可以存储在内部节点和叶子节点上。而在 B+Tree 中，记录只能存储在叶子节点上，而内部节点只能存储键。

B+Tree 的叶子节点以单链表的形式链接在一起，使搜索更加高效。

B+Tree 用于存储主存中无法存储的大量数据，由于主存大小有限，B+Tree 的内部节点（访问记录的键）存储在主存中，而叶子节点则存储在二级存储中。

B+Tree 的内部节点通常称为索引节点。下图是一颗阶数为 3 的 B+Tree。

B+Tree 的优点：

记录可在相同的磁盘访问次数内获取。
与 B-Tree 相比，树的高度保持平衡且较低。
可以按顺序访问 B+Tree 树种存储的数据，也可直接访问。
键用于索引。
由于数据存储在叶子节点上，因此搜索速度更快。

B-Tree 与 B+Tree 对比：

B Tree	B+Tree
搜索键不能重复存储	可能存在多余的搜索键
数据可存储在内部节点和叶子节点上	数据只能存储在叶子节点上
由于数据的存储，因此搜索过程会比较慢	由于数据都在叶子上，搜索速度相对更快
删除内部节点既复杂又耗时	删除内会很复杂，因为元素总是从叶子节点开始删除
叶子节点不能链接在一起	叶子节点链接在一起，使搜索更高效

B+Tree 的插入操作：

将新节点作为叶子节点插入。
如果叶子节点没有所需的空间，则拆分节点并将中间节点复制到下一个索引节点。
如果索引节点没有所需的空间，则拆分节点并将中间元素复制到下一个索引页。

B+Tree 的删除操作：

从叶子上删除键和数据
如果叶子节点包含的元素少于最小数量，则将该节点与同级节点合并，并删除它们之间的键。
如果索引节点包含的元数少于最小数量，则将该节点与同级节点合并，并下移它们之间的键。

红黑树

红黑树（red-black tree）是一颗二叉搜索树。红黑树种的每个节点都包含一个额外的位（bit），表示一种颜色，以确保在对树进行插入、删除等操作时，树是平衡的。

图

图（graph）可以定义为一组顶点（vertice）和连接这些顶点的边（edge）。图可以看作是一颗循环树，其中节点之间保持着复杂的关系，而不是父子关系。

有向图（Directed Graph）：边与方向无关。
无向图（Undirected Graph）：边构成有序的一对，代表从顶点 A 到 B 的特定路径。

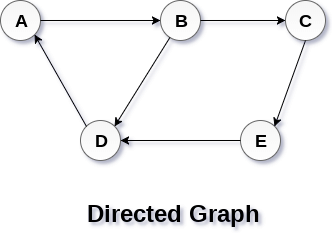
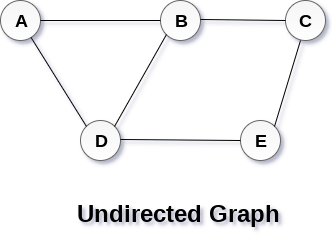
图的术语：

路径（path）：从初始节点到终点节点的节点序列。
封闭路径：初始节点与终点节点相同。
简单路径：所有节点都不同。
循环（cycle）：除第一个和最后一个顶点没有重复边或顶点的路径。
连通图：每两个顶点之间都存在路径。
完整图：每个节点都与其他节点相连。
加权图：每条边被分配了一些数据（如权重或长度）。
有向图
相邻节点
度（degree）：与该节点相连的边的数量。

图的表示

有两种表示方法：

顺序表示法（邻接矩阵表示法）：使用邻接矩阵来存储图。
链表表示法（邻接列表表示法）：使用临界列表来存储图。

顺序表示法

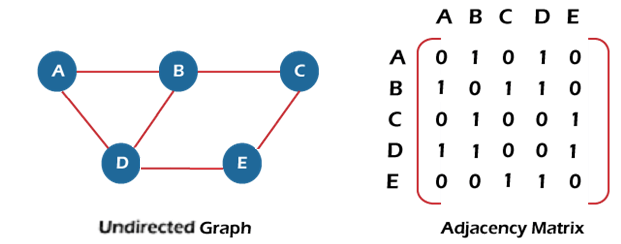
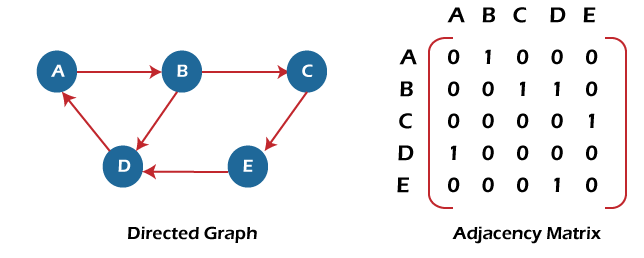
在顺序表示法中，使用邻接矩阵（adjacency matrix）来表示图中的顶点和边之间的映射。0 表示节点之间不存在关联，1 表示两条边之间存在路径。

如果图不存在自循环，则意味着邻接矩阵的对角项为 0。

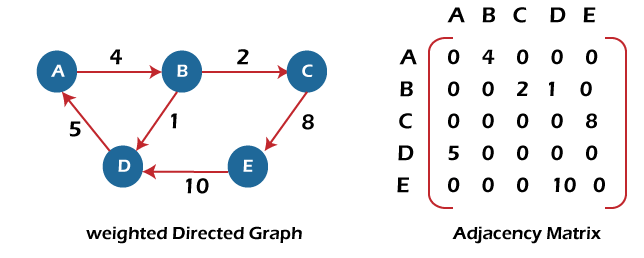
如果 adj[i][j] = w，则表示从顶点 i 到顶点 j 之前存在权重为 w 的边。

无向图的邻接矩阵表示。

有向图的邻接矩阵表示。

加权有向图的邻接矩阵表示。

链表表示法

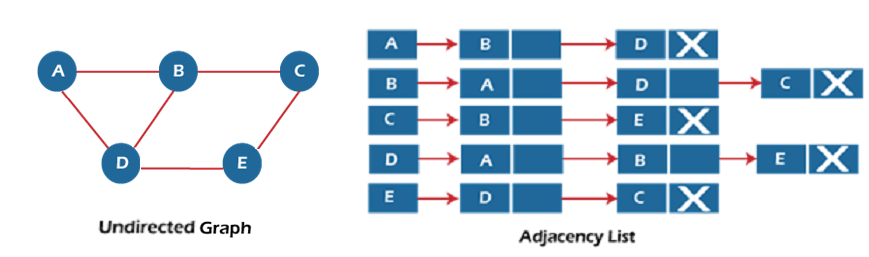
邻接列表（adjacency list）表示图，由于只需存储边的值，因此存储效率很高。

无向图的邻接列表表示。

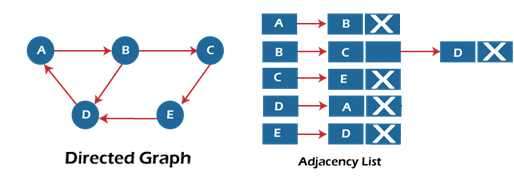
有向图的邻接列表表示。

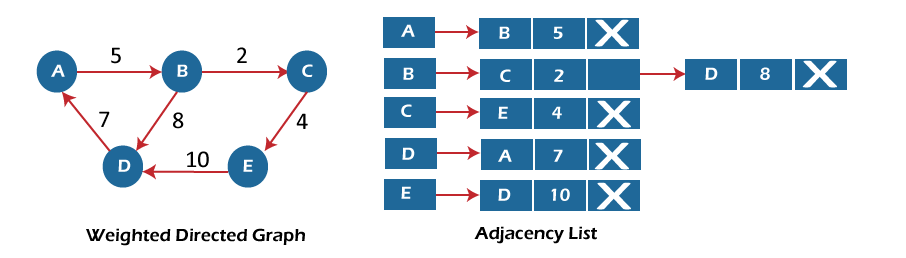
加权有向图的邻接列表表示。

BFS算法

BFS（Breadth-First Search），广度优先搜索是一种图遍历算法。它是一种递归算法，用于搜索树或图数据结构的所有顶点。

BFS 将图中的每个顶点分为已访问和未访问两类。它在图中选择一个节点，然后访问与所选节点相邻的所有节点。

BFS 算法的应用：

用于查找给定源位置的邻近位置。
在点对点网络中，用于查找所有的相邻节点。大多数 torrent 客户端都采用这种方法来查找网络中的种子和对等节点。
用于网路爬虫，创建网页索引。它从源网页开始遍历，并跟踪与网页相关的链接。
用于确定最短路径和最小生成树。
重复的垃圾回收。
计算网络流中的最大流量。

DFS算法

DFS（Depth-First Search），深度优先搜索是一种递归算法，用于搜索树或图的所有顶点。

由于栈数据结构具有递归性，因此可用来实现 DFS 算法。

DFS 算法的应用：

用于实现拓扑排序。
用于查找两个顶点之间的路径。
用于检测图是不是循环的。
用于一解谜题。
用于确定图是否为双链。

生成树

生成树是什么

生成树可定义为无向连接图的子图，它包括使用最少的边连接的所有顶点。它不存在循环，也不能断开。

生成树由 n-1 条边组成（n 是节点的数量）。生成树的边可能有权重，也可能没有。

一个完整的无向图可以有 $n^{n-2}$ 个生成树。n 是图中节点的数量。

生成树的应用

生成树用来寻找连接图中所有节点的最小路径。

集群分析
内网网络规划
计算机网络路由协议

生成树的示例

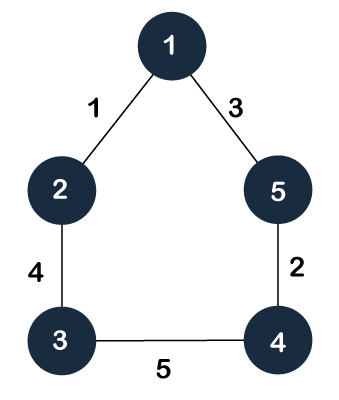
一个示例图有 5个节点，因此生成树有 4条边。一些生成树。

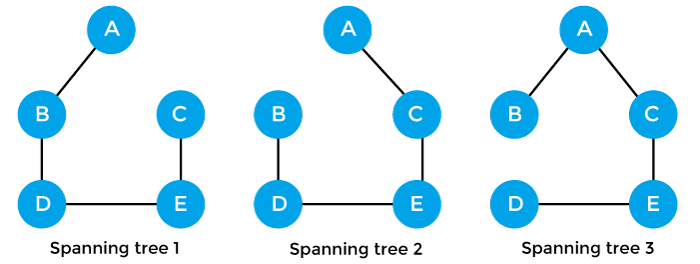
生成树的属性

连通图的生成树可能不止一颗
生成树没有环或循环。
生成树是最小连接，因此从生成树上移除一条边会使图形断开。
生成树是最大非循环的，因此在生成树上添加一条边会产生一个循环。
一个完整的图最多可以有 $n^{n-2}$ 个生成树。
生成树有 n-1 条边，n 为节点数。
生成树是连通图的子集，不存在断开图的生成树。

最小生成树

最小生成树可定义为边的权重之和最小的生成树。在现实世界中，这个权重可视为距离、交通负荷、拥塞程度和任何随机值。

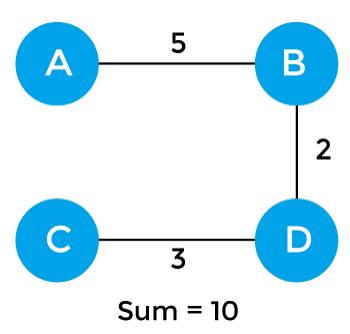
最小生成树可用来设计供水网络、电信网络和电网。
用来在地图中寻找路径。

搜索算法

数据结构的搜索算法。

线性搜索

线性搜索（Linear Search Algorithm）是在列表中查找某个特定元素的过程。

线性搜索（顺序搜索），是最简单的搜索算法。在线性搜索中，只需遍历整个列表，并将列表中的每个元素与要查找的项目进行匹配。

它被广泛用于从无序列表中搜索元素，最坏的时间复杂度为 O(n)。

线性搜索的时间复杂度

情况	时间复杂度
最好	O(1)
平均	O(n)
最坏	O(n)

二分查找

二分查找（Binary Search Algorithm），是一种在已排序列表中的有效工作的搜索技术。

因此，要使用二分查找在列表中进行搜索，必须确保列表已排序。如果列表未排序，必须先对列表进行排序。

二分查找将列表分为两半，然后将项目与列表中间的元素进行比较。如果匹配，则返回。不匹配，则在对半的列表中继续。

二分查找的复杂度：

情况	时间复杂度
最好	O(1)
平均	O(logn)
最坏	O(logn)

排序算法

数据结构的排序算法。

冒泡排序算法

Bubble Sort Algorithm

冒泡排序，工作原理是反复交换相邻元素，直到它们不在预定顺序内。就像水中的气泡的移动一样，水泡最终会上升到水面。同样，冒泡排序种的数组元素也会在每次迭代中移动到终点。

由于它的性能很差，因此主要用于教育目的。它的平均复杂度为 $O(n^2)$。

冒泡排序主要用于：

复杂度不重要
简单和简码是首选

桶排序

Bucket Sort Algorithm

桶排序，元素首先被分为为称为桶的组，然后用其他排序算法对他们进行排序。之后，元素以排序的方式聚集在一起。

优点：

减少了比较的次数。
由于元素分布均匀，它的速度近似较快。
每个桶都可以独立于其它桶进行处理。这意味着对初始数组进行排序后，经常需要对许多更小的数组进行排序。
将桶排序作为外部排序算法的能力。

缺点：

可能是一种稳定的排序算法，也可能不是。
如果有一个大数组，它就没用了，因为会增加成本。
它不是就地排序算法，因为需要额外的空间对桶进行排序。
不能使用数组中的所有数据类型，因为需要一种好的桶技术来对不同的数据类型进行排序。
当对输入的数据进行分组时，不建议执行桶排序，因为它不够充分。
在许多适合使用桶排序的情况下，可通过切换不同的专门排序算法来获得更优的性能。
桶排序的性能取决于桶的数量。

桶排序的平均复杂度为 $O(n+k)$，最差为 $O(n^2)$，n 是桶数。

桶排序常用场景：

使用浮点数值
当输入在一定范围内均匀分布时

梳状排序

Comb Sort Algorithm

梳状排序是冒泡排序的高级形式，冒泡排序比较所有相邻的值，而梳状排序则删除所有龟缩值或靠近列表末尾的小值。

它是一种基于比较的排序算法，是对冒泡排序的改进。冒泡中，被比较的元素间的间隙为 1，而梳状使用大于 1 的间隙来改进冒泡。在每个阶段完成后，间隙会被收缩因子 1.3 除以，迭代一直持续到间隙为 1。

平均和最坏的时间复杂度为 $O(N^2)$。

梳状排序的过程：

开始
计算间隙，如果为 1 进入步骤 5，否则步骤 3
迭代数据集，将每个项目与差距项目进行比较，然后转到步骤 4
如果需要，交换元素，否则转到步骤 2
打印排序后的数组
停止

梳状排序的特点：

基于比较的排序技术
就地排序技术，不需要额外的存储空间
类似于冒泡，但比冒泡更高效
如果元素的顺序不正确，则通过交换特定间隙的元素来完成排序

梳状排序的优点：

不需要额外空间
比冒泡更高效
逻辑非常简单易懂
本质上非常可靠
这种排序技术非常适合小型数据库

梳状排序的缺点：

最坏情况复杂度很差
对海量数据来说效率不高
梳状排序不稳定

计数排序算法

Counting Sort Algorithm

计数排序是一种基于特定范围之间键值的排序技术。

此技术不通过比较元素来执行排序。它像散列一样，通过计算具有不同键值的对象来执行排序。然后，它执行一些算术运算来计算每个对象在输出序列中的索引位置。计数排序不作为通用排序算法。

计数排序的平均和最坏复杂度 $O(n + k)$。

计数排序算法的应用：

当需要对包含较小整数且重复次数很多的数组进行排序时
当需要实现时间复杂性时
它能有效地处理元素范围有限且频繁重复的情况

计数排序算法的优点：

提供了基于比较的排序，如合并排序和快速排序，适用于范围与输入大小相当的输入。
此排序算法的实现很容易理解。
此排序算法具有稳定性，并能在排序输出中保留等值元素的原始顺序。

计算排序算法的缺点：

无法对十进制进行排序，这限制了它在涉及非整数数据的排序操作中的适用性。
当对大量数值进行排序时，它的效率就会很低。
作为一种非就地排序算法，计数排序需要额外的空间来存储辅助数据，会影响内存使用率。

堆排序算法

Heap Sort Algorithm

堆排序通过使用给定数组的元素创建最小堆或最大堆来处理元素。最小堆和最大堆标识数组的排序，其中根元素代表数组的最小或最大元素。

堆排序基本上递归执行两个主要操作：

使用数组元素建立堆 H。
重复删除第一阶段形成的堆元素。

什么是堆？堆是一颗完全二叉树。

什么是堆排序？堆排序是一种流行且高效的排序算法。从列表的堆部分逐个删除元素，然后将它们插入列表的排序部分。

堆排序是就地排序算法。

平均和最坏的时间复杂度为 $O(nlog^n)$。

堆排序的优点：

运行时不存在二次最坏情况。
是一种就地排序算法，空间复杂度为 $O(1)$
输入数据完全排序或几乎排序并不会降低复杂度

堆排序的缺点：

它不稳定，因为对堆的操作会改变键项的相对顺序。这是一种典型的不稳定排序算法。

插入排序算法

Insertion Sort Algorithm

插入排序的工作过程很简单。工作原理类似于手中扑克牌的排序。假设第一张牌已排序，然后选择一张未排序的牌。如果未排序的牌比第一张牌打，它将被放在右边，否则放在左边。同样，所有未排序的牌都会被取走，并放在它们的正确位置上。

插入排序也采取了同样的方法。原理是先取一个元素，然后在已排序数组中遍历它。

插入排序虽然简单，但并不适用于大型数据集，因为平均和最坏的时间复杂度都是 $O(n^2)$，最佳是 $O(n)$，n 是项的个数。插入排序的效率低于堆排序、快速排序、合并排序等其他排序算法。

插入排序的应用：

可对较小的数字列表进行排序
可借助插入排序来组织纸牌
按成绩对学生列表进行排序
为实时交易应用维护股票价格或汇率的排序列表

插入排序的步骤：

如果元素是第一个元素，则假定它已排序，返回 1。
挑选下一个元素，并将其单独存储在一个键中。
将 key 与排序数组中的所有元素进行比较。
如果排序数组中的元素比当前元素小，则移动到下一个元素。否则，将数组中更大的元素向右移动。
插入数值
重复操作，直到数组排序完毕

插入排序的优点：

实现简单
对小数据集有效
自适应，即适合已基本排序的数据集
对小型数据集的排序效率很高
还需要 $O(1)$ 的额外内存空间
能很好地处理已进行过大量排序的数据集
不会对具有相同键的元素的相对顺序产生任何影响

插入排序的缺点：

对大型数据集来说效率很低
与其他更先进的排序算法相比，它的性能并不理想

合并排序算法

Merge Sort Algorithm

合并排序是一种遵循 分而治之 方法的排序技术。类似于快速排序，它是最流行、最高效的排序算法之一。

它将给定的列表分为相等的两半，调用两半列表，然后合并已排序的两半列表。必须定义 merge() 函数来执行合并。

子列表被一次又一次的分成两半，直到列表无法继续分割。然后，将一对单元素合并成双元素，在此过程中对它们进行排序。排序后的两元素列表对再合并成四元素列表，如此反复，直到得到排序后的列表。

时间复杂度都是 $O(n*logn)$，空间复杂度 $O(n)$。

快速排序算法

Quick Sort Algorithm

快速排序是一种广泛使用的排序算法，在对一个包含 n 个元素的数组进行排序时，平均需要 nlogn 次比较。这是一种速度更快、效率更高的排序算法。

该算法采取分而治之的方法，将问题分解成子问题，然后解决子问题，再将结果合并起来解决原始问题。

Devide：首先选择一个枢纽元素，将数组分割或重写排列为两个子数组，使左边子数组中的每个元素都小于或等于枢纽元素，右边子数组中的每个元素都大于枢纽元素。
Conquer：递归，对两个子数组进行排序。
Combine：合并已排序的数组。

快速排序挑选一个元素作为中枢，然后围绕中枢元素进行分区。一个大数组被分成两个子数组，一个存放小于中枢的值，一个存放大于中枢的值。

最佳和平均时间复杂度为 $O(nlogn)$，最坏时间复杂度为 $O(n^2)$。空间复杂度为 $O(nlogn)$。

快速排序的应用：

不需要稳定排序时，可使用快速排序。
它是一种递归算法，因此所有调用优化都可以借助快速排序来完成。
此算法对缓存友好，因此用于数据时具有良好的局部性。
此算法可用于信息搜索，由于快速排序是最快的算法，因此它作为一种更好的搜索方式被广泛使用。

快速排序的优点：

这种算法的工作本质上是快速而有效的。
与其他算法相比，该算法的时间复杂度最高。
在空间有限的情况下，它是一个很好的选择。

快速排序的缺点：

这种算法本质上是不稳定的，因为它无法保持键值对的初始顺序。
当枢纽元素最大或最小，或所有组件大小相同时，它都无法正常工作。快速排序的性能可能会受到这些最坏情况的严重影响。
这是一个递归过程，因此很难实现。

阶乘排序算法

Radix Sort Algorithm

阶乘排序是用于整数的线性排序算法。在阶乘排序中，从最小有效数字到最大有效数字逐位排序。

阶乘排序的工作原理：

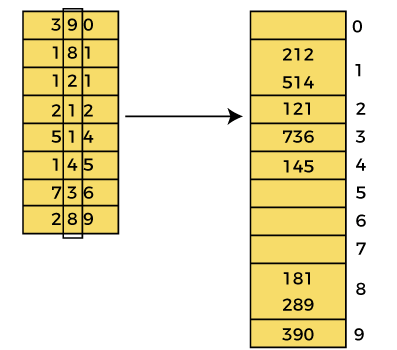
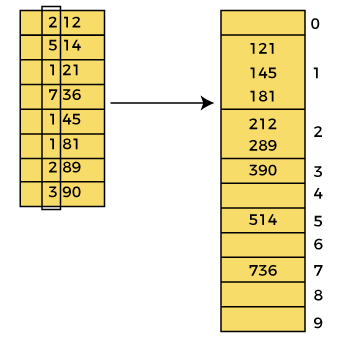
首先，必须从给定的数组中找出最大的元素（max），假设 x 是 max 的位数（如 736 共 3 位）。
然后，逐一对每个有效位进行排序。必须使用任何稳定的排序算法对每个有效位进行排序。（如 736，循环最多运行 3 次）

最坏时间复杂度 $O(nk)$

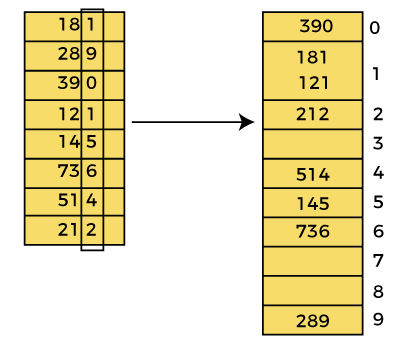
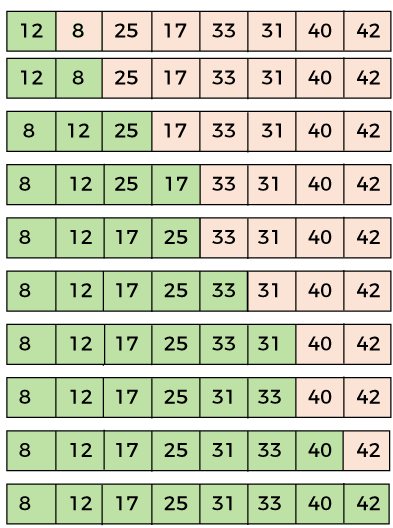
选择排序算法

Selection Sort Algorithm

在选择排序中，每次都会选择数组中未排序元素中最小的值，并将其插入数组的适当位置。这也是最简单的算法，它是一种就地排序算法。

在该算法中，数组被分为两部分，一部分已排序（放左边），一部分未排序（放右边）。

时间复杂度为 $O(n^2)$，其中 n 为项目数。因此，它不适合大型数据集。

选择排序常用于：

需要对一个小数组进行排序
交换成本并不重要
必须检查所有元素

1
2
3
4
5
6
7


12, 29, 25, 8, 32, 17, 40
8, 29, 25, 12, 32, 17, 40
8, 12, 25, 29, 32, 17, 40
8, 12, 17, 29, 32, 25, 40
8, 12, 17, 25, 32, 29, 40
8, 12, 17, 25, 29, 32, 40

选择排序算法的应用：

按成绩或姓名对学生进行排序
按日期或大小对文件进行排序
按升序或降序对扑克牌进行排序
电商中按价格对商品进行排序

选择排序的优点：

非常简单、易于理解和实施
对小型数据集或接近排序的数据很有效
元素排序无须额外的空间

选择排序的缺点：

对大型数据集来说效率很低
需要进行大量比较，因此运行速度较慢
是一种不稳定的排序算法。不稳定指它可能无法保持输入数组中相等元素的相对顺序

希尔排序算法

希尔排序是插入排序的一般化，通过比较相隔几个位置的元素来克服插入排序的缺点。

它是插入排序的扩展版本，改善了插入排序的平均时间复杂度，它是一种就地排序算法。它对中等规模的数据集很有效。

在插入排序中，元素每次只能移动一个位置。但希尔排序克服了这一缺点，它还允许移动和交换较远的元素。

此算法首选对相距较远的元素排序，然后缩小它们之间的差距。

目录